多くの方が両側検定と片側検定の違いについて混乱しているのではないでしょうか。これらの統計的な概念は、初めて耳にする方にとってはやや複雑であるため、理解するのが難しいと感じるかもしれません。
私自身も、正直なところ、両側検定と片側検定の使い分けについてよくわからなくなったので、今回あらためて考えてみることにしました。
どうも世の中の統計学の説明は間違いが含まれていることが多いらしく、しばしばTwitterなどで論争が巻き起こっている気がします。
今回の私の考察も間違っている可能性が十分にあるので、安易に間に受けないでください。
もし統計学に精通しているプロフェッショナルの方がいらっしゃいましたら、コメント欄で両側検定と片側検定の違いについて簡潔かつ分かりやすく解説していただけると大変ありがたいです。その知識を共有することで、私を含む多くの方が学ぶ手助けとなり、統計学の理解を深めることができるのではないかと思います。
ご協力をお願い申し上げます。
仮説検定の片側検定がよくわからない
帰無仮説と対立仮説が排反になっている場合には、
・帰無仮説が棄却される⇒対立仮説が採択される。
・帰無仮説が棄却されない⇒対立仮説が採択されない。
と考えるのは合理的だと思っています。疑問に思っているのは、その辺の教科書を開いてみても、
片側検定の場合、帰無仮説と対立仮説が排反になっていない(ことが多い)。
ということです。
このことについて説明がない本が多かったので、困りました。
考察
サイコロ投げを例にして、仮説検定を考えてみることにします。
霞む意識の中で、私はじっとりと冷たい床に背中を押し付けられていた。しばらくすると目が覚め、ぼんやりとした視界が次第に鮮明になっていく。周りを見ると、私以外にも様々な表情をした人々がいた。疑問と戸惑いに満ちたその空間は、何となく異様な雰囲気に包まれていた。 間もなく、壁に埋め込まれた大きなモニターが点灯し、機械的な声が響き渡った。
「ようこそ。ここはあなたがたが参加するデスゲームの会場です。」 一同は息を呑みながら画面を凝視する。画面上には、無機質なロボットがサイコロを持って微笑んでいた。
「ルールは簡単です。各参加者には、サイコロを振ってもらいます。出た目が6であれば勝ち。ただし、敗者は即座にこの場を去ることになります。」 その言葉に、会場には悲鳴や怒号が飛び交った。しかし、私はただ無感覚に立ち尽くしていた。
その時、モニターのロボットが続けて言った。「部屋の隅には大量のサイコロが用意されています。参加者は、それぞれ自分がゲームで使用するサイコロを選んでください。」
目を向けると確かに、部屋の片隅には無数のサイコロが積み上げられていた。それらは様々なサイズや材質で、ひとつひとつが異なる模様を持っていた。他の参加者たちはすぐにサイコロの山に向かって、自分の運命を託すサイコロを選び始めた。
私も足を動かし、サイコロの山に手を伸ばした。自分の選んだサイコロが、果たしてどれほどの運命を引き寄せるのか…。不安と期待が交錯する中、ゲームが始まる……!!
という状況を考えます。大量にあるサイコロの中で、どのサイコロを選べば良いかを考えることにします。適当に手に取ったサイコロについて、次の(1)(2)を調べることができると思います。
(1)サイコロは、6の目の出る確率が1/6ではない。
(2)サイコロは、6の目の出る確率が1/6より低い。
デスゲームに勝つためには(1)の場合を調べたところで、あまり意味はないのですが。
サイコロを100回ふってみて、6が出た回数を記録する。
10パーセントの確率で起きるようなことを、珍しいこととして扱うことにします。
(1)のケース
(1)のケースについて考えてみます。
帰無仮説:\(P(X = 6) = \frac{1}{6}\)
対立仮説:\(P(X = 6) \neq \frac{1}{6}\)
と立てて、\(P(X = 6) = \frac{1}{6}\) と仮定した場合に、サイコロを100回振ったときの6が出る回数の分布は、
二項分布\(B(100; \frac{1}{6})\)です。
こんな感じの分布になります。
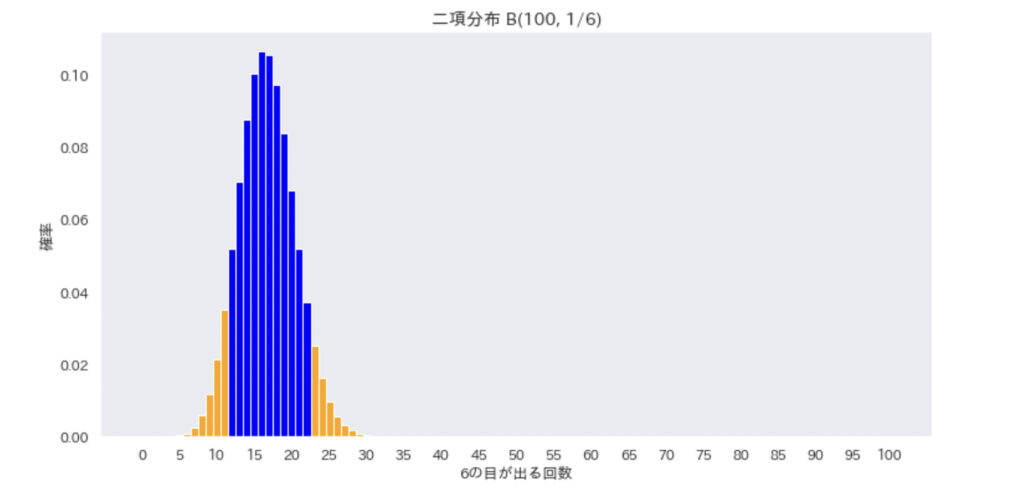
オレンジ色の部分をかき集めると大体10%くらいになるようにしています。
サイコロを100回振った結果、6の目が5回しか出なかったり、90回も出てしまった場合、これは非常に稀な出来事であり、その発生確率はおおよそ10%程度です。これを考慮すると、当初の仮説(帰無仮説)は信憑性が低く、代わりに対立する仮説を受け入れるべきと判断されます。
結果的に両側検定を行なったことになります。
(2)のケース
(2)のケースについて考えます。
帰無仮説:\(P(X = 6) \leq \frac{1}{6}\)
対立仮説:\(P(X = 6) > \frac{1}{6}\)
と仮説を立てます。
\(P(X = 6) \leq \frac{1}{6}\) と仮定した時に、10%の確率でおこる珍しいことを考えたいのですが、よくわからないですね。
そこで、\(P(X = 6) \leq \frac{1}{6}, \frac{1}{10}, \frac{1}{50}\) の、時の二項分布を見てみましょう。
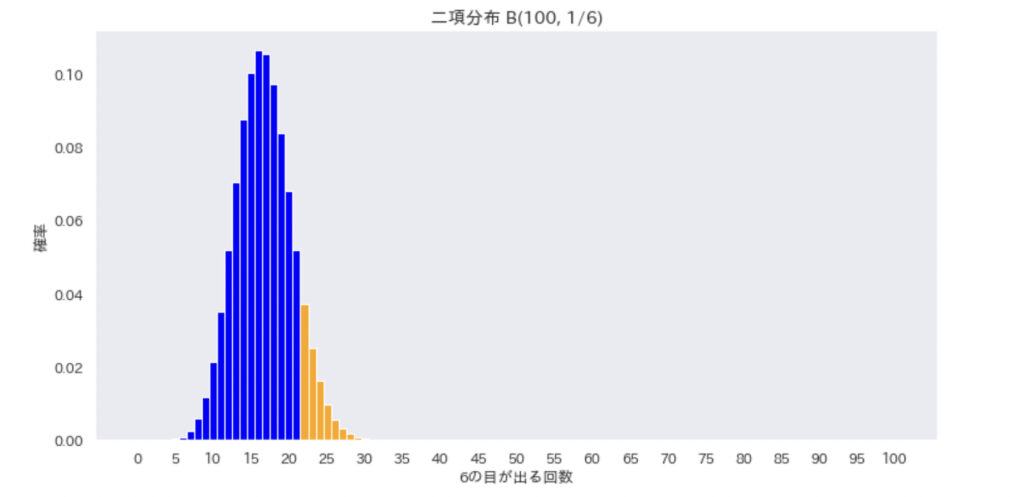
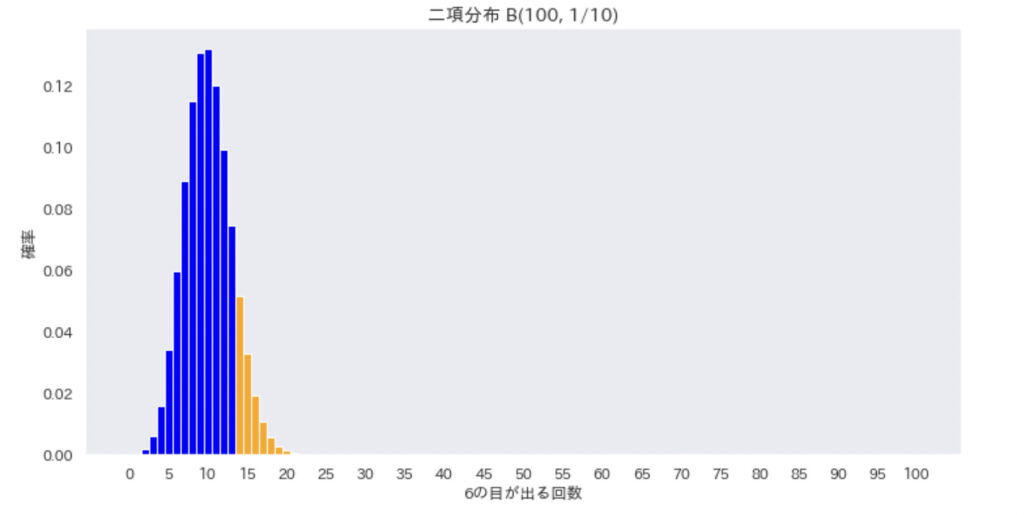
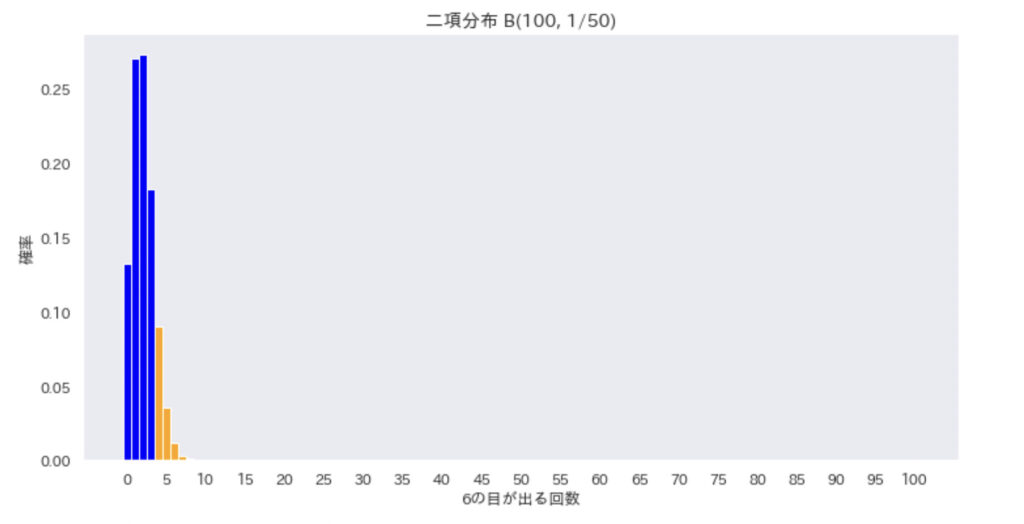
オレンジの部分を足し上げるとだいたい10%になるようになっています。
このことから、\(P(X = 6) = \frac{1}{6}\) だと仮定すると10%くらいの確率で起こる珍しいことと思えることは、\(P(X = 6) \leq \frac{1}{6}\)の時にも珍しいことだと思えるんだと思います。
一方で、\(P(X = 6) = \frac{1}{6}\) だと仮定したときに、珍しいわけではないことが起きたとき、
\(P(X = 6) \neq \frac{1}{6}\) という仮説は採択されないことになります。
\(P(X = 6) \neq \frac{1}{6}\) という仮説が採択されないなら、\(P(X = 6) > \frac{1}{6}\) という仮説も採択されないと考えるのは合理的だと思います。
というわけで、結局、\(P(X = 6) = \frac{1}{6}\) と仮定した場合だけを考えれば事足りるので、
帰無仮説:\(P(X = 6) = \frac{1}{6}\)
対立仮説:\(P(X = 6) > \frac{1}{6}\)
と考えても問題はないんだと思います。
最後に
推敲していないのでスッキリしない書き方になってしまいました。
もっとクリアな解説があったらコメントで教えてもらえれば幸いです。










コメント
コメント一覧 (1件)
云わば、両側検定と片側検定の違いは、所定の基準とのズレ幅について、両側検定は「スカラー的に」捉え、片側検定は「ベクトル的に」捉えていますよネ!!!
つまり、一定水準とのズレ幅を両側検定では、絶対値「Speed×Time」的に非負の数値化して捉え、このズレ幅が一定の正の数以下(又は厳密な整数±0)ならば、粗同じように、或いは変わっていないように見なすような扱いに成りますよネ!!!
つまり、ズレ幅を、「非負の」数値でしか表現せずに、つまり、「ズレ方向を考慮せずに」幅の大きさを「絶対値で」捉えます。
ですから、両側検定では、ズレ幅は、「スカラー」量で有り、「スカラー」把握されています。
これに対して、片側検定は、ズレ幅を「数値」表現して扱うような点こそ両側検定と同じですが、多いとか、増えたとか、優れているとかについての右側(上側)検定と、少ないとか、減ったとか、劣るとかの左側(下側)検定との2種類が有りますが、ズレ幅を前者では正の数で+表現し、後者では負の数で-表現します(両側検定でこそ両者とも正の数で+表現しますが)。
つまり、ズレ方について、片側検定では、幅(長さ)だけでは無くて、向き(ズレ方向)をも問題にします。
ですから片側検定は、ズレ幅をベクトル量「Velocity×Time」的に捉えたような表現だとは、云えない物でしょうか?
しかしながら、両側検定と片側検定の違いについて、前者は「スカラー的な」捉え方、後者は「ベクトル的な」捉え方、このような表現の説明が見受けられていませんが、このような説明の仕方は如何な物でしょうか?
取り敢えず、御提案迄。