信頼性理論における全信頼基準の導出をわかりやすく解説

2025年5月25日

この記事では信頼性理論における全信頼基準の導出をわかりやすく解説します。

全信頼基準(full credibility standard)とは、
サンプル平均が、真の平均値から誤差\(k\)(割合です)以内に入る確率が\(1-\alpha\)以上になることを保証するために必要なデータ数の目安です。
どういうことかというと、最初に\(\mu, \alpha\)を与えた上で、
\begin{align*} P(| \frac{1}{n} \sum X_i – \mu | \leq k \mu\) \geq 1 – \alpha \al\end{align*}
を満たす最小の\(n\)はいくつですかということです。

実際に、
\(\frac{1}{n} \sum X_i = \bar X \)が正規分布\(N(\mu, \sigma^2)\)に従うような状況を考えます。すると、
\begin{align*} \bar X \sim N(\mu, \frac{\sigma^2}{n} )\end{align*}
ですので、正規化をしてやることで、
\begin{align*} P(| \bar X – \mu | \leq k \mu\) = P( \frac{| \bar X – \mu|}{\sqrt{ \frac{\sigma^2}{n}}}\leq k \mu \frac{1}{\sqrt{ \frac{\sigma^2}{n}}}\) \end{align*}
となります。正規化をすると標準正規分布に従うことから、標準正規分布の上側\(\alpha/2\)点を\(z_{\alpha/2}\)と表記することにすると、
\begin{align*}k \mu \frac{1}{\sqrt{ \frac{\sigma^2}{n}}} \geq z_{\alpha/2} \end{align*}
であることがわかるので、
\begin{align*} n \geq \left( \frac{z_{\alpha/2} \sigma}{k \mu}\right)\end{align*}
であることがわかります。

もっと感覚的に理解すると、
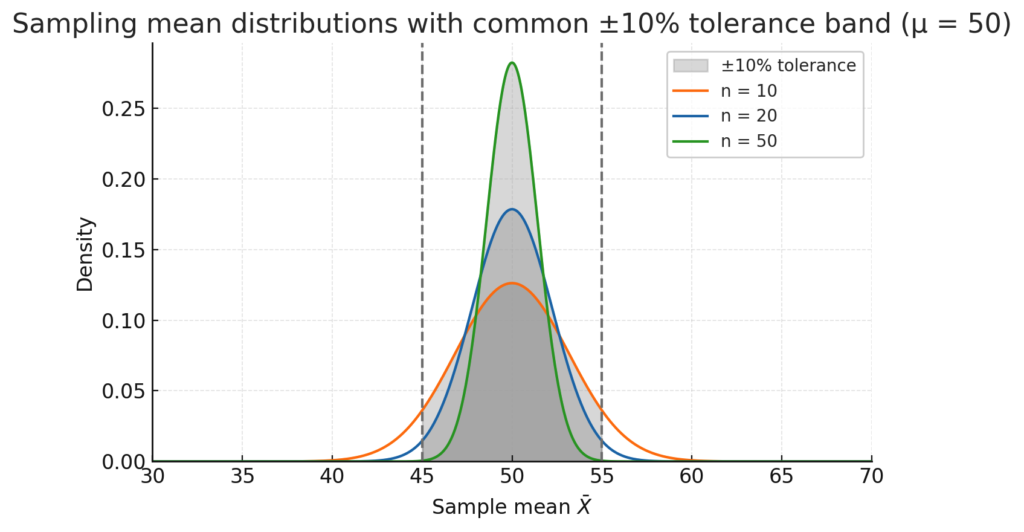
例えば、\(\mu = 50\)で、\(k = 10%\)のような状況では、
許容される誤差は\(50 * 10% = 5\)であるので、
\begin{align*} 45 \sim 55 \end{align*}
まではオッケーだよ〜という許容される範囲を最初に設定しておくことになります。
そしてサンプル平均が、この許容される範囲にできるだけ高い確率で入るようにしようと思うと、
\begin{align*} n \rightarrow \infty \infty\end{align*}
とどんどん上げていけばよいことがわかります。\(n\)を例えば999999999999999くらいにしたら、もう分散がめちゃくちゃ小さくなるのでほとんど真の平均付近にとどまることがわかりますが、もう少し丁寧に上げていくと、どれくらいあげればよいかを考えていることになります。
以下に示すグラフは、\(n\)を10, 20, 50と変えた時の\(\bar X\)の分布ですが、
\(n\)が大きくなるにつれて、45~55におさまる確率が大きくなっていることがみてとれます。