e^{-x}は急減少関数でないがe^{-x^2}は急減少関数であることの証明

e^{-x}は急減少関数でないが、e^{-x^2}は急減少関数であることの証明

$e^{-x}$ が急減少関数になるかどうかを調査しました！

簡単のために$\mathbb{R}\to \mathbb{R}$ のような一変数関数を考えることにします。

急減少関数

急減少関数とは、無限遠方での減衰が非常に早い関数のことです。今回は急減少関数の定義として次のものを採用します。

任意の$n,m\in \mathbb{N}$ に対して、

$$\begin{array}{r}\underset{|x|\to \mathrm{\infty }}{lim}|x^m(\frac{d^n}{d{x}^n}f)(x)|=0\end{array}$$

をみたす関数を急減少関数といいます。他にも同値な定義はありますが、ここでは言及しないことにします。

e^{-x}が急減少関数でないことの証明

e^{-x}が急減少関数でないことを証明してみようと思います。

落ち着いて考えてみましょう。$e^{-x}$ のグラフを見てください。

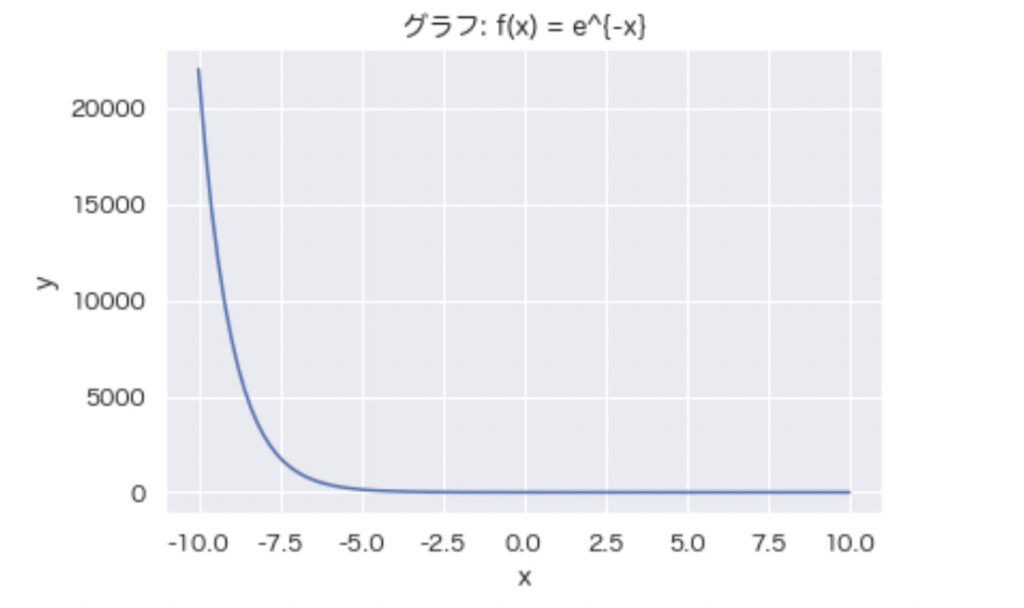
明らかにマイナス方向では減衰してません。実際、

$$\begin{array}{r}{e}^{-x}\to \mathrm{\infty }(x\to –\mathrm{\infty })\end{array}$$

となるので、急減少関数ではありませんね。証明は終了です。

e^{-x^2}が急減少関数であることの証明

続いて、$e^{-x^2}$ が急減少関数です。そのことを証明してみましょう。

$e^{-x^2}$ を微分すると$-2x{e}^{-x^2}$ です。もう一度微分すると、$-2e^{-x^2}+4x^2{e}^{-x^2}$ です。こんな感じで$m$ 回微分すると結局$\frac{d^n}{d{x}^n}{e}^{-x^2}=p(x)e^{-x^2}$ と、適当な$n$ 次の多項式$p$ を用いて表されます。

$$\begin{array}{r}\underset{|x|\to \mathrm{\infty }}{lim}|x^n|\frac{p(x)}{e^{x^2}}=\underset{|x|\to \mathrm{\infty }}{lim}\frac{\text{定数}}{e^{x^2}}=0\end{array}$$

となります。ロピタルの定理を繰り返し使いました。これで証明は終了です。

ついでに$e^{-x^2}$ のグラフをみてみましょう。

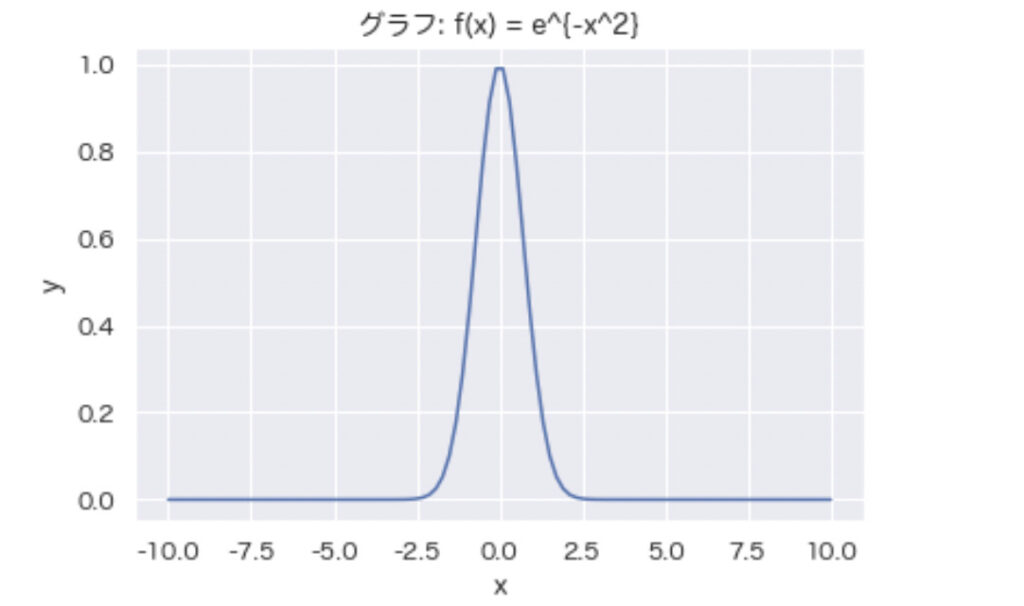
どうでしょうか。$e^{-x}$ と違ってマイナス方向でも減衰していますよね。

あわせて読みたい記事