単射・全射・全単射の違いをわかりやすく解説

写像が単射・全射・全単射であるとはどういうことかについて、具体例を交えてわかりやすく解説します。大学数学の初めの段階では、関数や写像といった基本的な概念を学びますが、特に、単射であるか全射であるかということは非常に重要ですので、必ずマスターしておきましょう。

単射・全射・全単射の違いをわかりやすく解説

この記事では\(X, Y\)で集合を表すことにします。

単射とは？わかりやすく解説

写像が単射であるとはどういうことでしょうか。まずは定義から確認しましょう。

図に表してみると、以下のようになります。

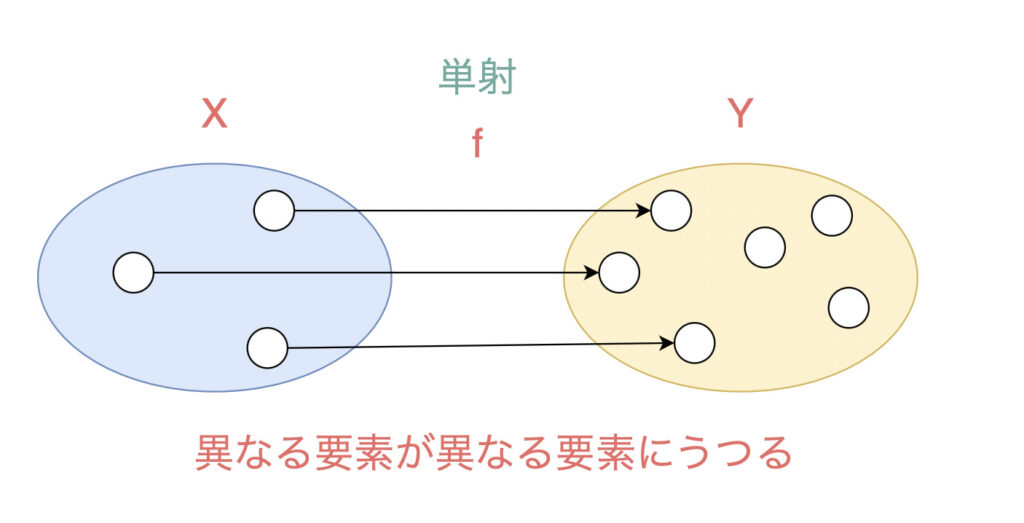
すなわち、単射とは「Xの異なる要素」が写像によって「Yの異なる要素」にうつるとき、単射であるといいます。

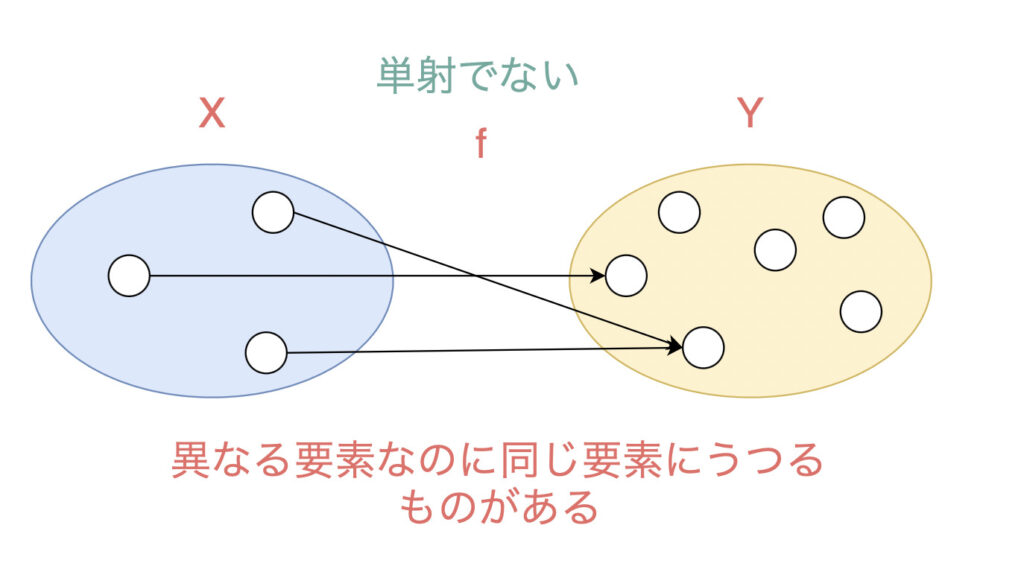
一方で単射でないとはどういうことでしょうか。
\(f: X \rightarrow Y\)が単射でないということは、\(x, x^\prime \in X\)で
\begin{align*} x \neq x^\prime \quad \textrm{かつ} \quad f(x) = f(x^\prime)\end{align*}
を満たすものが存在するということです。

単射という概念の現実世界における重要性

数学における写像の概念は、現実世界の多くの現象やプロセスに対応させることができます。
特に、単射写像は情報の損失や重複に関連する興味深い側面を持っています。

写像が単射である場合、元の集合\(X\)の情報が像の集合\(Y\)に移る際に、情報が落ちていないと考えることができます。異なる元が同じ像に写されることがないため、写像を明示できるならば\(Y\)の情報から\(X\)の情報を完全に復元することが可能です。

しかし、考えている写像が単射でない場合、重複して同じものに写っている要素が存在するので、\(Y\)の情報から\(X\)の情報を完全に復元することができないことがあります。

この概念を具体的な例として、画像処理における「ぼかしフィルター」に当てはめて考えてみましょう。

ぼかしフィルターは、画像のピクセルを周囲のピクセルの情報と足し合わせて平均で置き換える処理です。この処理により、画像全体がぼんやりとした外観になります。

しかし、この「ぼかしフィルター」を「あらゆる画像の集合」から「あらゆる画像の集合」への写像と考えると、単射ではないことがわかります。
なぜなら、画像としては異なっていても、平均を取ることで同じ画像になってしまうものが存在するからです。
この重複によって、ぼかされた後の画像から元の画像を完全に特定することはできないのです。

同じく、モザイク処理された画像から、モザイクを除去することを考えると、同じ問題が発生します。
モザイク処理によって細かい情報が失われ、異なる元の画像でも同じモザイク化された画像になる可能性があります。
従って、100%元の画像を復元することはできず、あくまで元の画像を類推することしかできないのです。

このような視点からみると、単射でない写像は、情報の圧縮や変換の際における制約や限界を数学的に捉える有用な手段となります。それはコンピュータサイエンスや画像処理、通信工学などの分野でも直接的な応用があります。単射写像の概念は、これらの現実的な課題を理解する上での鍵となり、数学の抽象的な理論が具体的な技術や応用にどのように関連するかを示す美しい例でもあります。

全射とは？わかりやすく解説

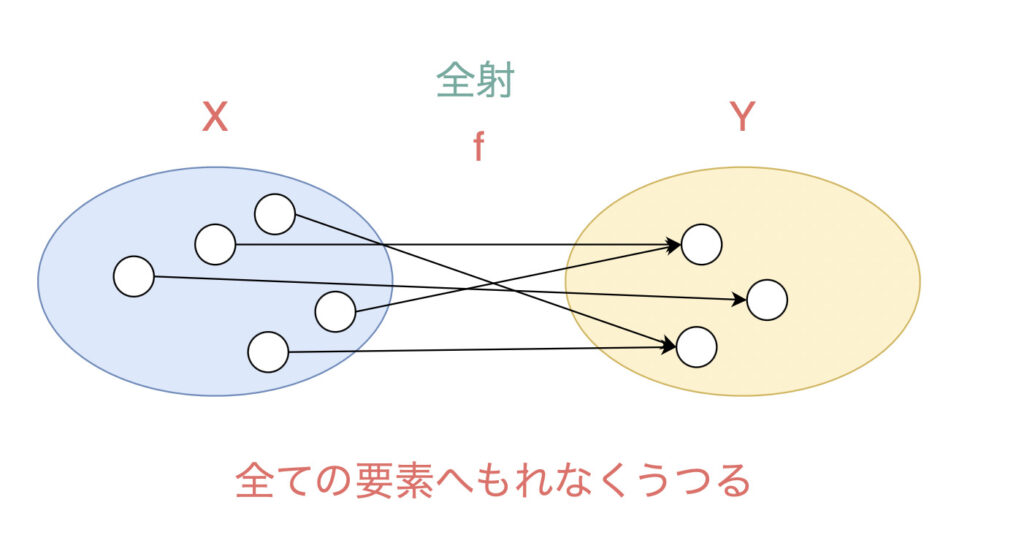
写像が全射であるとはどういうことでしょうか。まずは定義から確認しましょう。

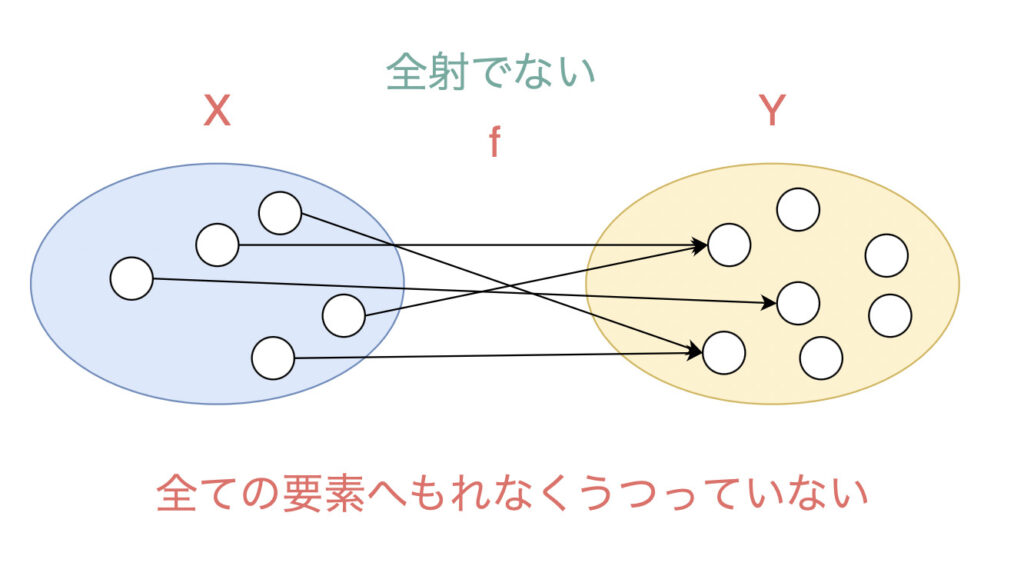
一方で全射でないとはどういうことでしょうか。
\(f: X \rightarrow Y\)が全射でないということは、\(y \in Y\)で
どんな要素\(x \in X\)も\(f(x)\)が\(y\)と一致しないものが存在するということです。

補足ですが、全射でない写像も、写像の終域を制限することでかならず全射になるようにすることができます。
もちろん、全射になるように終域を制限するので全射になるのは当たり前ですが。
このことは、写像が単射であるとか全射であるとかいう性質は、写像の始域と終域の組に対して定まる性質であるということです。

例えば、\(\sin\)という関数は、\(\mathbb R\)から\(\mathbb R\)への写像として考えると全く全射ではありません。
しかしながら、写像の終域を\([-1, 1]\)だと考えることにすると、\(\sin\)は全射になります。
このように、写像の性質を考える上で始域と終域がなんであるかを考えることは不可欠となります。

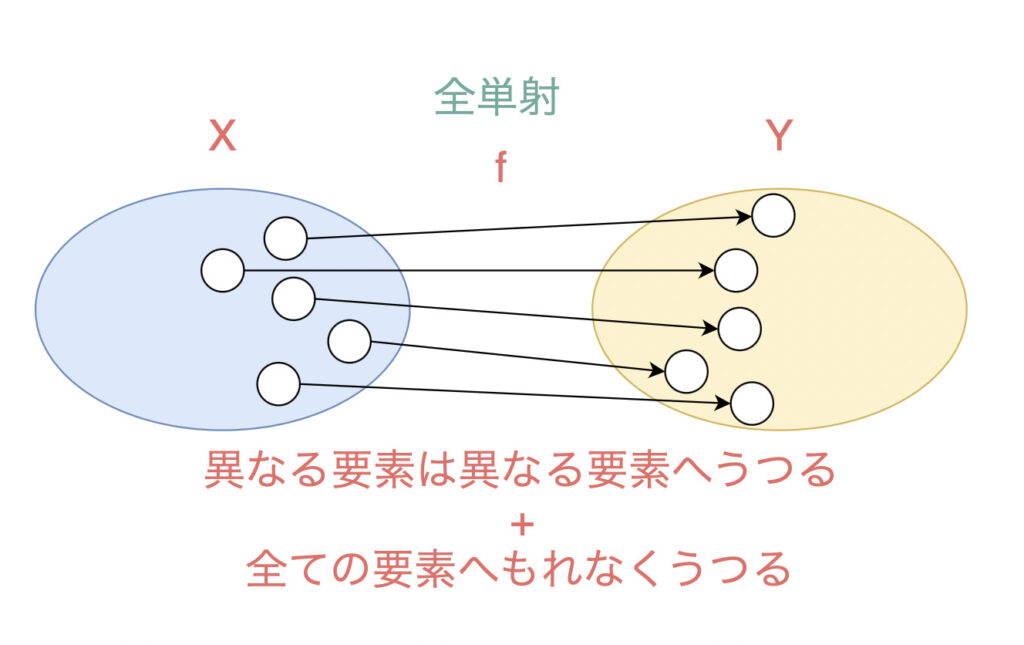
全単射とは？わかりやすく解説

補足ですが、任意の写像が終域を適当に変更することで全射とすることができたように、
単射である写像は、終域を制限してやることで全単射となるように出来ます。

例えば\(f(x) = \sqrt{x}\)という写像を考えてみましょう。
\(f\)は\([0, \infty)\)から\(\mathbb R\)への写像として考えると単射です。
ここでさらに、終域を\([0, \infty)\)とすると、\(f\)は全単射となります。

繰り返しになりますが、写像の性質は正確には始域と終域にも依存した性質であるということがわかります。

単射と単射の合成が単射であることの証明

実際、任意の\(x, x^\prime \in X\)に対して\(x \neq x^\prime\)であるならば、
\(f\)が単射であるので、\(f(x) \neq f(x^\prime)\)となります。
そして、\(g\)も単射であるので、\(g(f(x)) \neq g(f(x^\prime))\)となります。
これはすなわち\(g \circ f\)が単射であることを意味しています。これで証明は終了します。

全射と全射の合成が全射であることの証明

実際、任意の\(z\in Z\)に対して\(g\)が全射であるので、\(y \in Y\)で\(g(y) = z\)であるものが存在します。
そして、\(f\)が全射であるので、\(x\in X\)で\(f(x) = y\)であるものが存在します。
つまり、\(g(f(x)) = g(y) = z\)が成り立ちます。
これは\(g \circ f\)が全射であることを意味しています。これで証明は終了します。

合成が単射であるならばそれぞれの写像は単射か？

実際、\(f\)が単射でないと仮定すると、\(x, x^\prime \in X\)で
\(x\neq x^\prime\)なのに\(f(x) = f(x^\prime)\)であるものがとれます。
すると、\(g(f(x)) = g(f(x^\prime))\)となります。
これは\(g\circ f\)が単射であることと矛盾します。これで証明を終了します。

ここで注意したいことは、\(g\)が単射であるということは言えないという点です。
例えば、\(f: \{1\} \rightarrow \{a, b\}\)と\(g: \{a, b\} \rightarrow \{x, y, z, w\}\)をそれぞれ
\(f(1) = a\)、\(g(a) = w,\,\, g(b) = w\)として定めます。
すると\(f\)は単射で、\(g\)は単射でないことが確認できます。
しかしながら、合成\(g \circ f: \{1\}\rightarrow \{x, y, z, w\}\)は単射であることが確かめられます。
従って、合成が単射であるからといって両方の写像が単射であるということは言えません。

合成が全射であるならばそれぞれの写像は全射か？

実際、\(g\)が全射でないとすると、
\(z \in Z\)で任意の\(y \in Y\)に対して\(g(y) \neq z\)となるものが存在します。
従って、任意の\(x \in X\)に対して\(f\circ g (x) \neq z\)となるので、
これはすなわち\(g\circ f\)が全射でないことを意味するので、矛盾します。これで証明を終了します。

ここで注意したいことは、\(f\)は全射となるとは限らないということです。
例えば、\(f: \{1\} \rightarrow \{a, b\}\)と\(g: \{a, b\} \rightarrow \{x\}\)をそれぞれ
\(f(1) = a\)、\(g(a) = x,\,\, g(b) = x\)として定めます。
すると、\(g \circ f\)は全射であるのですが、\(f\)は全射ではなく、\(g\)は全射であることが確認できます。
従って、合成が全射であるからといってそれぞれの写像が全射であるとは限りません。

真に単調な関数が単射であることの証明

\(\mathbb R\)から\(\mathbb R\)への関数\(f\)は
\begin{align*} x < x^\prime \Rightarrow f(x) < f(x^\prime)\end{align*}
を満たす時に真に単調増大であるといいます。

証明は明らかで、\(x, x^\prime \in X\)が\(x\neq x^\prime\)であるならば、
\(x< x^\prime\)か\(x^\prime < x\)なのですが、
\(x< x^\prime\)ならば\(f(x) < f(x^\prime)\)なので\(f(x) \neq f(x^\prime)\)だし、
\(x^\prime < x\)ならば\(f(x^\prime) < f(x)\)なので\(f(x) \neq f(x^\prime)\)であるからです。

単射と全射の普遍性による特徴づけ

単射と全射という性質を普遍性によって特徴づけることもできます。
このことは、集合を対象とし、写像を射とすることで定まる集合の圏において、単射はモニックと、前者はエピックと同値であることと対応しています。

証明：

(1)ならば(2)を示しましょう。\(g_1, g_2: Z\rightarrow X\)で\(f\circ g_1 = f\circ g_2\)かつ\(g_1 \neq g_2\)であるものが存在すると仮定します。
適当な\(z\in Z\)で\(g_1(z) \neq g_2(z)\)であるものが存在します。
\(f(g_1(z)) = f(g_2(z))\)なので、\(f\)が単射であることに矛盾します。

(2)ならば(1)を示します。任意に\(x, y \in X\)で\(f(x) = f(y)\)であるものをとります。
\(\varphi_x , \varphi_y: \{*\} \rightarrow X\)という1点集合からの写像を、
\begin{align*} \varphi_x (*) = x, \varphi_y(*) = y\end{align*}
により定めると、\(f \circ \varphi_x = f \circ \varphi_y\)なので、\(\varphi_x = \varphi_y\)となります。
従って、
\begin{align*} x =\varphi_x (*) = \varphi_y (*) = y \end{align*}
となるので、\(f\)が単射であることが示されました。

証明：

(1)ならば(2)から示します。\(g_1, g_2: Y \rightarrow Z\)で\(g_1 \circ f = g_2 \circ f\)であるものをとります。
\(f\)が全射であることから任意の\(y \in Y\)に対して、\(x \in X \)で\(f(x) = y\)であるものがとれます。
\begin{align*} g_1 (y) = g_1 \circ f (x ) = g_2 \circ f(x) = g_2(y) \end{align*}
より\(g_1 = g_2\)がいえます。

(2)ならば(1)を示します。
\(g_1, g_2 : Y \rightarrow \{ 0, 1\}\)を
\begin{align*}g_1 (y) = 0 \quad (\forall y \in Y) \\ g_2 (y) = \begin{cases} 0 & y \in f(X) \\ 1 & y \notin f(X) \end{cases} \end{align*}
と定めると、\(g_1 \circ f = g_2 \circ f\)であるので、\(g_1 = g_2\)です。
これは\(y \notin f(X) \) である\(y \in Y\)が存在しないことを意味するので、\(f\)は全射です。

線型写像の単射の判別方法

ベクトル空間の間の線形写像に対しては、単射を判別する簡単な方法があります。
ここで\(\mathbb R\)を係数体とするベクトル空間\(V, W\)の間の写像\(L\)が線型写像であるとは、
任意の\(v, v^\prime, \,\, r, r^\prime \in \mathbb R\)に対して
\begin{align*} L(r v + r^\prime v^\prime ) = r L(v) + r^\prime L(v^\prime) \end{align*}
が成り立つことをいいます。

\(L(v) = 0 \,\, \Rightarrow v = 0\)
が成り立つとします。
背理法を用いることにして、\(L\)が単射でないとすると、\(v, v^\prime \in V\)で\(v \neq v^\prime\)なのに\(L(v) = L(v^\prime)\)であるものが存在します。
\(L(v- v^\prime ) = L(v) – L(v^\prime) = 0\)なので、\(v – v^\prime = 0\)となります。
これは\(v \neq v^\prime\)に矛盾します。

逆に、\(L\)が単射であるとします。
背理法を用いることにして、\(v\in V\) で\(Lv = 0\)かつ\(v \neq 0\)であるものが存在すると仮定します。
すると、\(0 \neq v\) なのに\(L(0) = L(v)\)となるので、\(L\)が単射であることに矛盾します。