ソローモデルとは？計算式や定常状態をわかりやすく解説！！

ソローモデルは、マクロ経済学における経済成長理論の一つで、1956年にロバート・ソローによって提唱されたものです。このモデルは、経済がどのように成長し、時間とともにどのように変化するかを理解するためのフレームワークを提供します。

ソローモデルとは？計算式や定常状態をわかりやすく解説！！

経済成長を分析するために広く利用されているソローモデルは、資本蓄積、労働人口の成長、技術進歩といった要素を組み合わせて、経済全体の成長を説明します。このモデルは、特に長期的な経済成長の動向を捉えるのに適しており、多くの政策立案や経済学的予測に役立てられています。

ソローモデルの離散的なモデリング

ソローモデルは標準的には生産関数としてコブダグラス型生産関数を採用してモデリングします。
今回は時間に関するパラメータが離散的な状況を考えることにします。

ソローモデルについて誰でも直ちにわかること

ソローモデルについて誰でも直ちにわかることをいくつか考察してみましょう。
ここは、間違いなく誰でもわかるので読み飛ばしても大丈夫です。

ソローモデルにおいては、生産関数が特定の関係性を示しています。
具体的には、資本量 \(K_t\) が増加すると、生産量 \(Y_t\) も大きくなります。
これは、資本が生産の重要な入力要素であるため、より多くの資本が利用可能であれば、それに比例して生産能力も向上するという直感的な理解に基づいています。

また、技術水準 \(A_t\) と労働力 \(L_t\) が増加する場合も同様です。
技術水準が高いほど、生産効率が向上し、同量の資本と労働に対してより多くの生産物を生み出すことができます。
一方、労働力が多ければ、それだけで生産可能な量も増加します。
したがって、\(A_t\) や \(L_t\) が増えれば、それに応じて \(Y_t\) も大きくなると考えられます。

これらの関係性は、ソローモデルが少なくともトンデモモデルではないということを意味しています。
もし、資本量が増加するほど\(Y_t\)が減少するようなモデリングになっていれば、トンデモモデルだったことでしょう。

ソローモデルにおける定常状態の計算: 効率労働あたりの資本

ソローモデルを考察するために、適当に式を変形したりしてみましょう。天下り的ですが、

\begin{align*} k_t := \frac{K_t}{A_t L_t}\end{align*}

という記号を導入してみます。
\(A_t, L_t\)を掛け算した\(A_t L_t\)という値は、効率労働と言われます。従って、\(k_t\)は効率労働あたりの資本と言われます。

すると、ソローモデルの式は次のように変形できます。

\begin{align*} Y_t = K_t^\alpha \left(A_t L_t \right)^{1-\alpha} = k_t^\alpha A_t L_t \end{align*}

また、遷移式から得られる情報がないかあれこれと変形を試してみましょう。

\begin{align*} k_{t+1} &= \frac{K_{t+1}}{A_{t+1} L_{t+1}}
\\&= \frac{(1-\delta)K_t + sY_t}{(1+g)A_t (1+n)L_t}
\\&=\frac{(1-\delta)K_t}{(1+g)A_t (1+n)L_t} + \frac{s Y_t}{(1+g)A_t (1+n)L_t}
\\&= \frac{1 – \delta}{(1+g)(1+n)}k_t + \frac{sk_t^\alpha A_t L_t }{(1+g)A_t (1+n)L_t}
\\&= \frac{1 – \delta}{(1+g)(1+n)}k_t + \frac{s }{(1+g)(1+n)}k_t^\alpha \end{align*}

このような式が得られたならば、初期時刻\(t=0\)において\(k_0\)が絶妙な値であるならば、
\begin{align*} k_0 = k_1 = k_2 = \cdots \end{align*}
が成り立つようにできることがわかるでしょう。

この絶妙な値を求めるためには、
\begin{align*} \kappa = \frac{1 – \delta}{(1+g)(1+n)} \kappa + \frac{s }{(1+g)(1+n)} \kappa ^\alpha \end{align*}
を満たす\(\kappa\)を求めればよいことがわかります。

\(\kappa=0\)のとき、実際にこの式が成り立つことが確かめられます。
つまり、\(K_0 =0\)であれば、\(k_0 = k_1 = k_2 \cdots = 0\)です。

\(\kappa \neq 0\)であるようなケースを探してみましょう。
\begin{align*} \kappa = \frac{1 – \delta}{(1+g)(1+n)} \kappa + \frac{s }{(1+g)(1+n)} \kappa ^\alpha\end{align*}
の両辺を\(\kappa\)で割ると、
\begin{align*} 1 = \frac{1 – \delta}{(1+g)(1+n)} + \frac{s }{(1+g)(1+n)} \kappa ^{\alpha – 1}\end{align*}
ですので、\((1+g)(1+n)\)をかけると、
\begin{align*} (1+g)(1+n) = 1- \delta + s \kappa ^{\alpha – 1} \end{align*}
が得られます。つまり、
\begin{align*} \kappa^{\alpha – 1} &= \frac{(1+g)(1+n) – (1 – \delta) }{s}
\\&= \frac{g + n + gn + \delta }{s} \end{align*}
を解いて、
\begin{align*} \kappa = \left( \frac{g + n + gn + \delta }{s}\right)^{\frac{1}{\alpha – 1}} \end{align*}
と求められます。

従って、次のような命題が得られます。

もちろん、次のことも同時に言えます。

定常状態への収束をグラフで確認してみましょう

では、定常状態へ収束するかどうかを調べるために、グラフをプロットしてみましょう。

\(\alpha = 0.25\)
\(\delta = 0.05\)
\(s = 0.25\)
\(g = 0.05\)
\(n = 0.1\)
という設定で、
\begin{align*} k_{t+1} = \frac{1 – \delta}{(1+g)(1+n)}k_t + \frac{s }{(1+g)(1+n)}k_t^\alpha \end{align*}
と、
\begin{align*} k_{t + 1} = k_t\end{align*}
のグラフをそれぞれプロットしてみます。

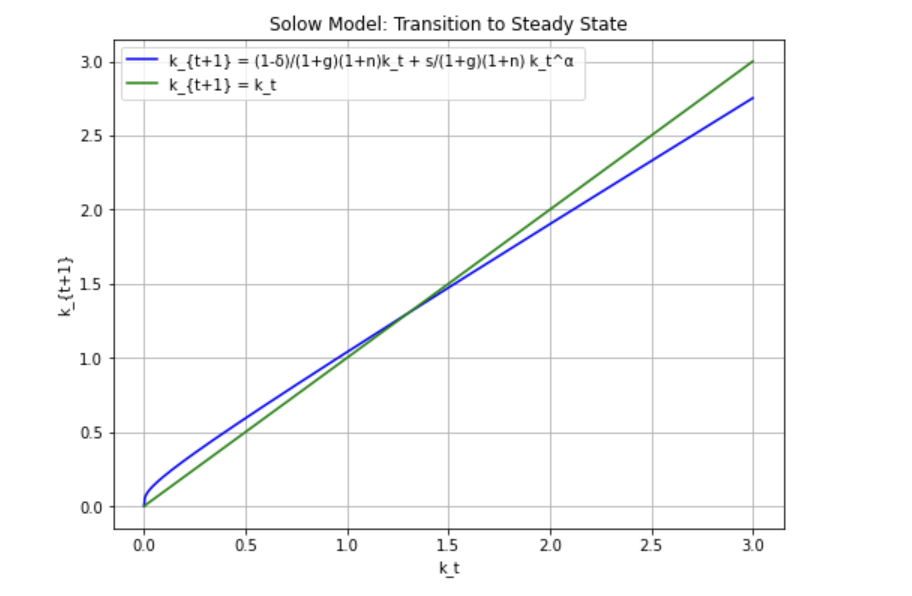
力学系における蜘蛛の巣図法の考え方(蜘蛛の巣図法という用語自体は知らなくても大丈夫です)により、\(k_t\)は確かに定常状態へと収束していくことがわかります。
どういうことかというと、\(k_t\)をどんな値からスタートしても、
\(k_t, k_{t+1}, k_{t+2}, \ldots\)と次々に求めていくと、次第に青線と緑線の交点へと値が近づいていくことになります。そして、一度交点における値をとると、ひたすら交点における値をとりつづけるので、これは定常状態であるということがわかります。

ソローモデルの連続的なモデリング

ここまでは離散的なモデリングについて考えてきましたが、連続的なモデリング方法についても考えてみましょう！
そのためには、単に差分を微分に置き換えれば良いです。最も簡単な状態を考えるため、登場するすべての関数は微分できることとしておきます。

離散的な場合と同様に
\begin{align*} k(t) = \frac{K(t)}{A(t)L(t)} \end{align*}
という記号を導入することにしましょう。効率労働あたりの資本です。

また、
\begin{align*} y(t) = \frac{Y(t)}{A(t)L(t)} \end{align*}
という記号も導入しましょう。効率労働あたりの生産です。

徐に、\(k\)を微分して、\(k\)の変化が何に依存するかを確認してみましょう。
\begin{align*} \dot k(t) &= \frac{\dot K(t)A(t)L(t) – K(t)\dot A(t)L(t) – K(t)A(t) \dot L(t) }{(A(t)L(t))^2}
\\&= \frac{\dot K(t)}{A(t)L(t)} – \frac{K(t)}{A(t)L(t)} \frac{\dot L(t)}{L(t)}- \frac{K(t)}{A(t)L(t)} \frac{\dot A(t)}{A(t)}
\\& =\frac{\dot K(t)}{A(t)L(t)} – \frac{K(t)}{A(t)L(t)} n- \frac{K(t)}{A(t)L(t)} g
\\&= \frac{-\delta K(t) + sY(t)}{A(t)L(t)} – k(t) n- k(t)g
\\&= \frac{-\delta K(t)}{A(t)L(t)} + \frac{sY(t)}{A(t)L(t)} – k(t) n- k(t)g
\\&= -\delta k(t) + s y(t) – n k(t) – g k(t) \end{align*}
となります。すなわち、
\begin{align*} \dot k(t) = s y(t) – (\delta + n + g) k(t) \end{align*}
となります。この式が意味することは、
\begin{align*} s y(t) = (\delta + n + g) k(t) \end{align*}
であるならば、\(\dot k(t) = 0\)となり、\(k(t)\)は時間が経過しても変化しないということになります。
\(sy(t)\)は効率労働あたりの投資量であるため、次のような帰結を得られます。

ソローモデルにおける貯蓄率の変化

ソローモデルに従う世界において、貯蓄率の変化が何を引き起こすかを考えてみましょう。

まず初めに、
\begin{align*} y(t) &= \frac{Y(t)}{A(t)L(t)} \\&= \frac{(K(t))^\alpha (A(t)L(t))^{1-\alpha}}{A(t)L(t)}
\\&= \left(\frac{K(t)}{A(t)L(t)} \right)^\alpha
\\&= (k(t))^{\alpha} \end{align*}
であることを確認しておきましょう。従って、
\begin{align*} s y(t) = s (k(t))^\alpha \end{align*}
です。

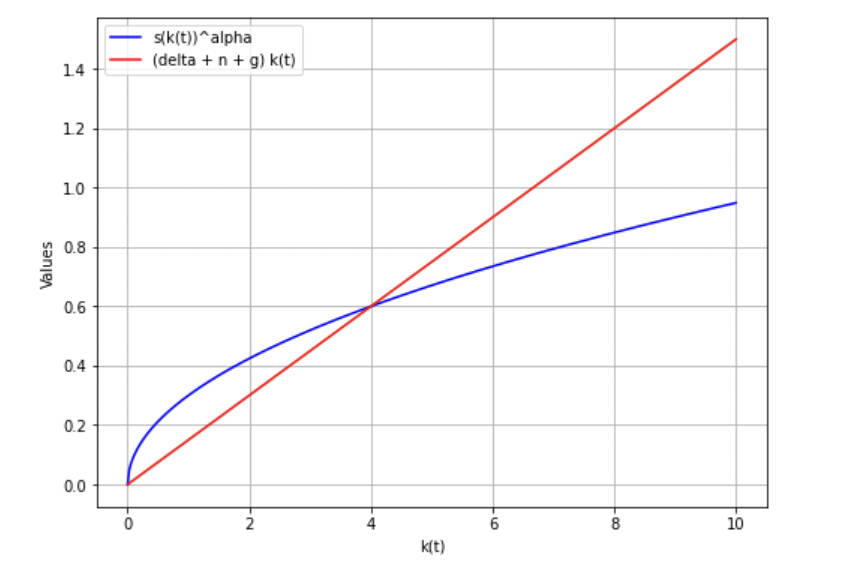
\(\dot k(t) = 0\)となための条件
\begin{align*} s y(t) = (\delta + n + g) k(t) \end{align*}
は
\begin{align*} s (k(t))^\alpha = (\delta + n + g) k(t) \end{align*}
と書き換えることができます。
青線を\(s (k(t))^\alpha\)、
赤線を\((\delta + n + g) k(t)\)としてグラフに描画してみましょう。
交点が条件を満たすような\(k(t)\)です。

$lates s$が\(s^\prime ( > s)\)に変化したとします。
新たに青点線で\(s^\prime (k(t))^\alpha\)を表すことにします。
すると、交点を与えるk(t)の値が右に変化していることがわかるでしょう。

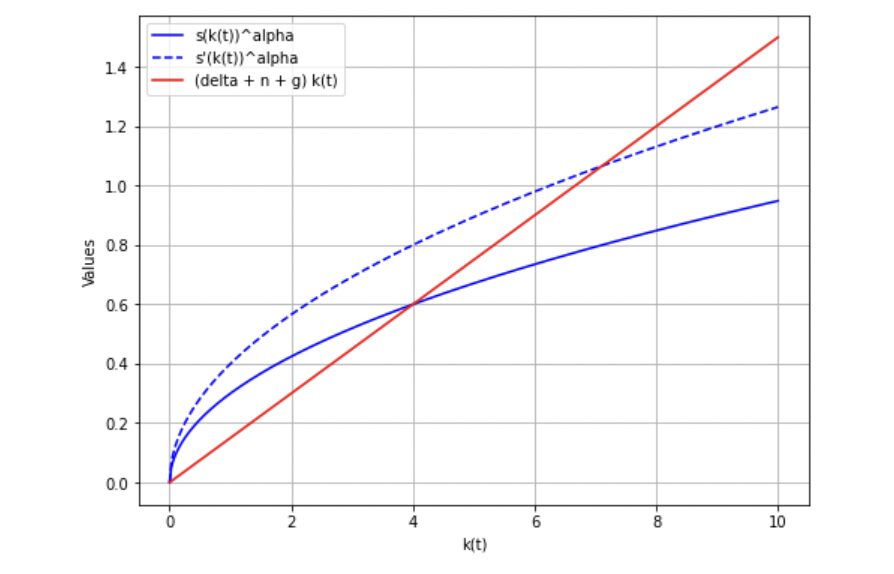
\(k(t)\)が定常であった状態
\begin{align*} \dot k(t) = s y(t) – (\delta + n + g) k(t) = 0 \end{align*}
から、\(s\)が上昇し, \(s^\prime\)になると、
\begin{align*} \dot k(t) = s^\prime y(t) – (\delta + n + g) k(t) > 0 \end{align*}
このようになり、\(k(t)\)は上昇していく状態になります。
その後、再び\(k(t)\)が定常になります。

マクロ経済学の定番参考図書

理論と実証のバランスを重視し、最先端の理論で経済問題を解き明かす。マクロ経済学を本当に理解したい学部上級、大学院生必携の決定版テキスト。

https://www.nippyo.co.jp/shop/book/5250.html

あわせて読みたい記事